最近在做一个项目,其中有文件同步的需求,并且文件会经常更新。如果每次都将文件全量上传,那么每次都上传未改动的部分,肯定会浪费大量的流量。因此采用对文件分块的方式,每次上传前比较文件块的差异,仅将差异部分上传即可,这样会减少很大一部分流量。比较完的差异部分大致可用下面的结构来表示:
type Difference struct {
FileName string
Blocks []int
}其中,FileName是已修改文件的文件名,Blocks是int类型的数组,是差异文件块序号的集合。
经提醒,其实上述结构还有优化的余地。
int类型至少可再分为两种:int32和int64,即用32bit或64bit来表示一个整数。他们可表示的整数范围显然是不同的。拿int32来说,如果1号块和2号块有修改,那么它们的二进制形式如下:
// 1
0000 0000 0000 0000 0000 0000 0000 0001
// 2
0000 0000 0000 0000 0000 0000 0000 0010可以看到,除了最右边的两bit是不同的,其余的各bit均相同,那么这一部分数据其实是可以不必要传输的,如果是int64,那么浪费的资源就更多了。随着差异块的个数增多,利用率也随之下降。
所以可以考虑用位图的方式进一步压缩。
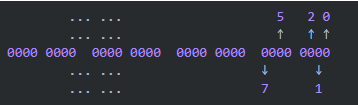
如上图所示,使用一串二进制的第一位来标识第一个块即0号块,第二位来标识1号块,依此类推。我们用1来表示某个块是更改了的,0来表示未更改的块。这样原来用来存储一个不同块的序号的4个字节现在可以存储32个不同块,8倍的压缩率可以说是很厉害了。并且,随着差异块的个数增多,利用率也随之提升。
然而,事实真的如此丰满吗?
考虑一下这种情况:假设某个文件有1G,在这个文件的末尾添加一个字节的内容。
那么按int32数组存储,我们需要4个字节。按位存储,我们需要2^30/2^3 = 2^27字节,这个差距就大了去了!因此用位图的方式,随着差异块的最大块号的增大,利用率也随之下降的。
根据以上条件,我们知道一定可以找到一个平衡点,在这个平衡点处,两者的效率会几乎一致,那么如何找到这个平衡点?
经过以上过程,可以知道影响利用效率的因素有两个:1. 差异块的个数,2. 差异块的最大块序号。假设最大差异块的块序号为y,差异块的个数为x,那么需要的字节数如下表:
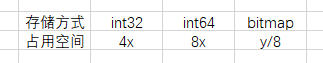
当两者需要的空间相等时,4x=y/8,即y=32x,函数图如下:
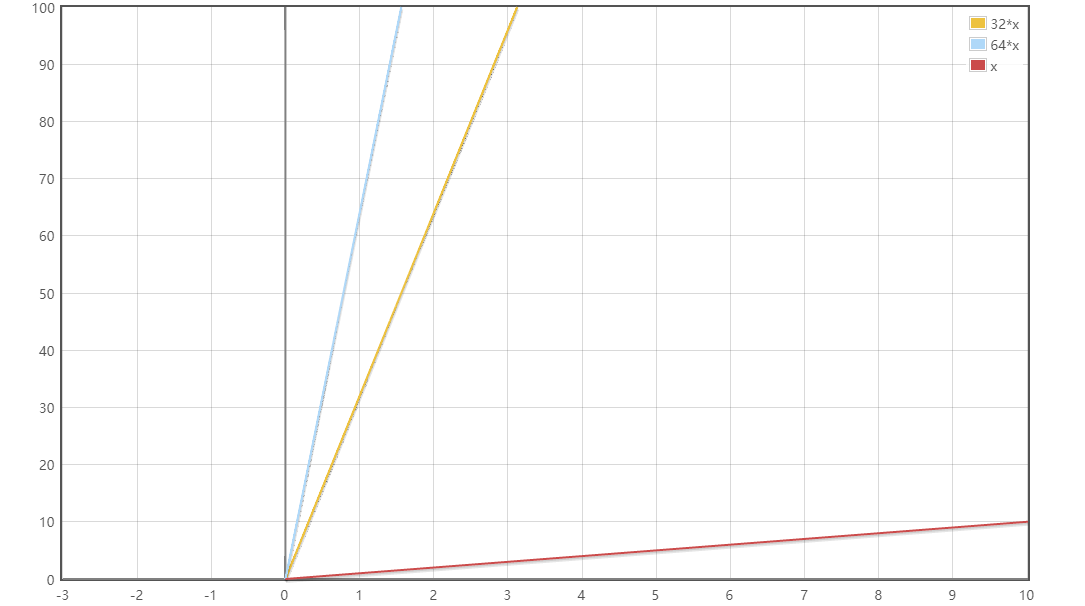
可以看出在黄色线的上方,使用int32存储比较省空间,在黄色线的下方,使用bitmap存储比较省空间。(论证部分较简单,此处省略)
这里其实还有个条件,那就是,最大差异块的序号一定是大于差异块的个数的,也即y>x。因此,可得出以下结论:
- 在黄色线的上方,使用int32存储效率较高。即最大块序号大于差异块个数的32倍时,应当采用int32数组存储。
- 在黄色线的下方,红色线的上方,使用bitmap存储的效率较高。即最大块序号小于差异块个数的32倍时,应当采用bitmap存储。
至于什么时候最大块序号大于差异块个数的32倍,那要结合业务特点及文件类型来判断。当文件更新较为频繁时,更新内容可能较少,差异块个数可能就少,这时应当用int数组。当文件为文本文件时,尤其是日志类型文件,那么对文件的操作基本为追加操作,改动的是最后一些块,此时最大块序号可能较大,因此也应考虑用int数组。当文件为二进制文件时,可能为可执行文件,差异部分可能会比较多并且较均匀分布在整个文件中,此时就应该考虑使用bitmap。总之,不同存储方法要根据具体情形来决定!
在写本文的时候,深深的被理科的美给吸引了。美在它是自洽的;美在它是确定的;美在它是互通的。
